表計算ソフトを使い、東京都のコロナ感染症新規感染者数の２週間予測をしてみた（更新停止中）

更新の停止(2022年1月13日）

渋谷の人出データと東京都の新規感染者数の相関が高いことを利用し、このブログで２週間後の感染者数を予測してきましたが、今後は更新を停止いたします。その理由は、コロナウイルスの変化のスピードに追いつけなくなっていることでし。また、渋谷の人出データが年末年始などの日常と異なる時期には予測が大きくずれることもあります。

先ず、変化に追いつけなくなっている件ですが、デルタ株までは新株が見つかってから感染者の割合が増える迄に感染力を推定し予測式を調整しなおすための時間があったのですが、オミクロン株では感染力の推定ができる前に感染が広がってしまい、全く予想が不可能になってしまいました。オミクロン株は、もはや、これまでの新型コロナ感染症とは異なる感染症とみなすほうが妥当かもしれません。

年末年始などにずれる件については、そもそも渋谷の人出データは、朝６時から夕方６時までの人出をカウントしているため、夜の人々の活動が反映されていないこと、年末年始の人々の活動も反映していないらしいこと、等様々な理由が想像されます。

2021～2022の年末年始には、上の二つが重なり、急激な増加がまったく予想できませんでした。また、オミクロン株では感染から発症までの期間が短くなっているらしく又検査に要する日数も短くなっているため、２週間予測も実態は１週間予測が妥当なようです。更に、オミクロン株では無症状者がかなり多いようですので発表される感染者数と実際の感染者（市中にいる陽性者）との乖離が大きくなっているものと思われます。このような状況では、コロナ新規感染者数の２週間予測は無意味になったものと考え、今後の更新を停止することにしました。今迄、よく外れるのにも関わらずご覧頂いた方々、ありがとうございました。

始めに

新型コロナウイルスの感染経路に関しては、飛沫感染が中心であり、人の動きが感染状況に大きく影響するらしいこと、又、感染した日からPCR検査により陽性と判断され新規感染者数として発表されるまで２週間近く遅れるらしいこと、が分かっています。これらの事実に基づき、こことは別のブログの『新型コロナウイルスへの対応　その８　「人出のデータから今後の感染者数の傾向を予想する方法」』という記事に、渋谷のスクランブル交差点の人出のデータから２週間後の東京都における新規感染者数の変化傾向を予測する方法を書きました。　

ここでは、上のブログに書いた方法により表計算ソフトを用いて新規感染者数の週毎の予測をしてみました。

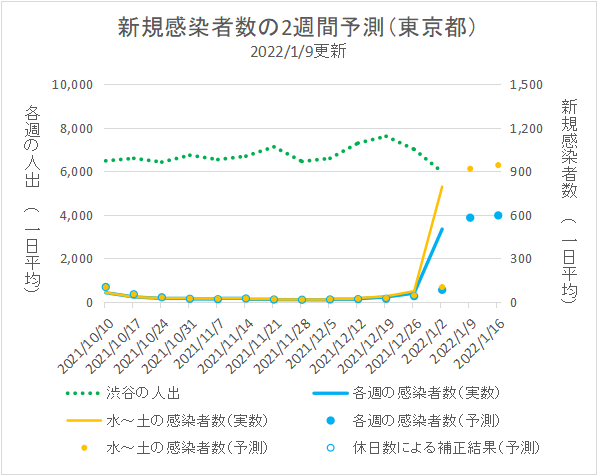
下のグラフで、横軸の年月日は週の始めの月曜日です。緑色の破線は渋谷の人出のデータです。水色の折れ線は日々発表される東京都の新規感染者数の週平均（日曜から土曜までの7日間の平均）です。水色の丸印はその翌週と翌々週の予測です。オレンジ色の折れ線は、水曜日～土曜日の4日間の日々発表される新規感染者数の平均で、オレンジ色の丸印は予測です。東京都は土曜日と日曜日の検査数が少ないため、日、月、火曜日はその影響を受け、新規感染者数が少なくなる傾向にがあります。一方、水～土曜日は比較的多めの新規感染者数となりますので、その4日間の平均で感染の状況を見るのも一つの目安かと思います（その週の最多人数が予想しやくなります）。なお、平日が休日になった場合なども感染者数に大きな影響を受けますが、予測の計算に際しては休日については考慮していませんので、参考まで、平日が休日になった場合の補正結果を白抜きの丸印で表しています。

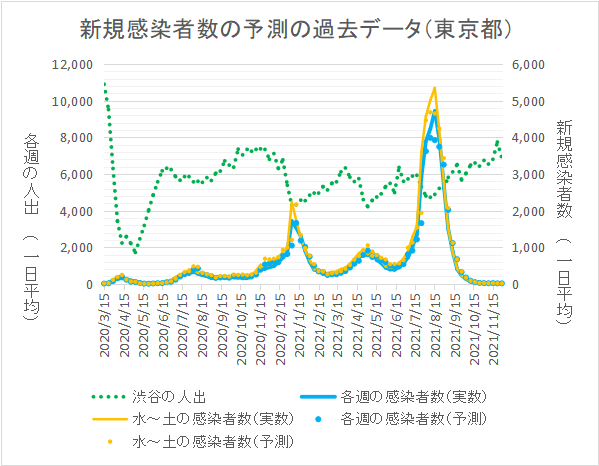
なお、年末年始、５月の連休、その他大きなイベント時などには、予測が大きくずれます。渋谷の人出から東京都全体の人々の活動を推測するのが無理な場合のあることを示すようです。2022年1月第1週は桁違いのズレになりました。下の２枚めのグラフは、第1波の頃からの過去のデータです。上に書いたような時には予測が大きく外れやすい傾向がみえます。又、通常でも１割程度の誤差はあってもおかしくありませんので、おおらかに見てください。なお、折れ線と丸印のズレが予測の誤差になります。

［追記］このブログ記事では、当初、データを表で表していましたが、見やすくするために、4月26日に表からグラフに変更しました。また、その後、グラフの更新とともに説明も修正してきたため、一貫しない記述となってしまいましたので、以下、10月に大幅に加筆修正しました。

＜予測について＞

ここで言う予測とは、感染から検査で見つかるまで平均2週間弱の遅れがあるため、今後２週間に見つかる可能性のある新規感染者はもう既に決まっており、今迄の2週間の人出の様子から、今後２週間の新規感染者数が推測できる、ということです（実際は、2週間ではなく1週間半程度かもしれません）。従って、数学的（信号処理的）には予測ではありませんが、今後も予測という言葉を使います。

予測を行うに当たり、基本的には上にも示しました記事『新型コロナウイルスへの対応　その８　「人出のデータから今後の感染者数の傾向を予想する方法」』に記載した式を用いました。その式で必要になる日々の東京都の新規感染者数はNHKのサイトからダウンロードして使っています。渋谷スクランブル交差点の人出データはNHKのサイト（Agoopの人流データを使用）から目視で読み取っていますので正確さはありません。なお、何故、渋谷のデータが全東京都民の接触状況を表すのかはっきりとした根拠はありませんが、経験に基づき使っています。渋谷の人出データは、午前6時から午後6時までの1時間あたりの平均値なのだそうで、通勤、通学、買い物、遊び等の人々が適当にミックスされており、たまたま東京都の平均的な接触状況に近くなっているものと思われます。又、東京都の近隣の県では、大まかには東京都の傾向と似た傾向を示すようです。

＜計算式について＞

上のブログ記事では、感染対策、気候の変化、ワクチンの効果、変異株の影響などは、すべてまとめて式の中の基本再生産数R0とパラメータｑに埋め込んでいました。しかし、ここでは、以下のようにしています。
　　Re＝R0＊（変異株の影響）＊（ワクチンの効果）＊（人出）
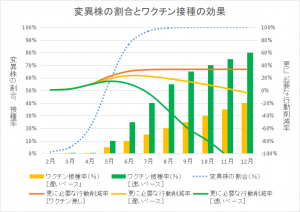
ここで、Reは実効再生産数、R0は基本再生産数です。R0として、変異株の影響等の式内の要素以外の、感染対策等その他の様々な要因を組み込んであります。変異株としてアルファ型、デルタ型を考慮し、ワクチンの効果としてその時々の累積接種率を使い、人出にはNHKの渋谷のデータを使っています。又、式は実効再生産数の形で表現しておりますが、ここでは、週毎の感染者数の変化として解釈し直しています。上の式のR0、（変異株の影響）、（ワクチンの効果）は、このブログの別記事「表計算ソフトを使い、コロナ変異株に対するワクチンの効果をシミュレーションしてみた」の計算結果を用いています。このブログ記事では、渋谷の人出からRe（ここでは、週毎の増減の割合）を求め、この先2週間の新規感染者数を予測しています。

＜予測結果の信頼性＞

新規感染者数はそもそも信頼性に欠けるデータではありますし、統計的にもかなりのバラツキがあります。また、渋谷の人出と東京都の新規感染者数の関係も、単に相関がそれなりにある、というだけであって直接の因果関係がある、というわけでもありません。従って、年末年始や大型連休、オリンピック等の大きなイベント、などの前後で誤差が大きくなってます。誤差の理由として、そのような場合に渋谷の人出のデータでは東京都全体の人の動きに対応できていないことの他に、感染者数が急激な増減に伴いPCR等検査数が大きく変化していることも考えられます。しかし、その変動は予測はできませんので、休日についてのみ白抜きの丸印で補正を表してはいますが、実際にはどの程度が感染者数に影響しているのか不明です。

以上の点から、上のグラフにはある程度の誤差が避けられないことをご理解ください。実感としては、平常時は大体10％程度の誤差、大きな波の前後では20％程度の誤差があるようです。